Skip to main content

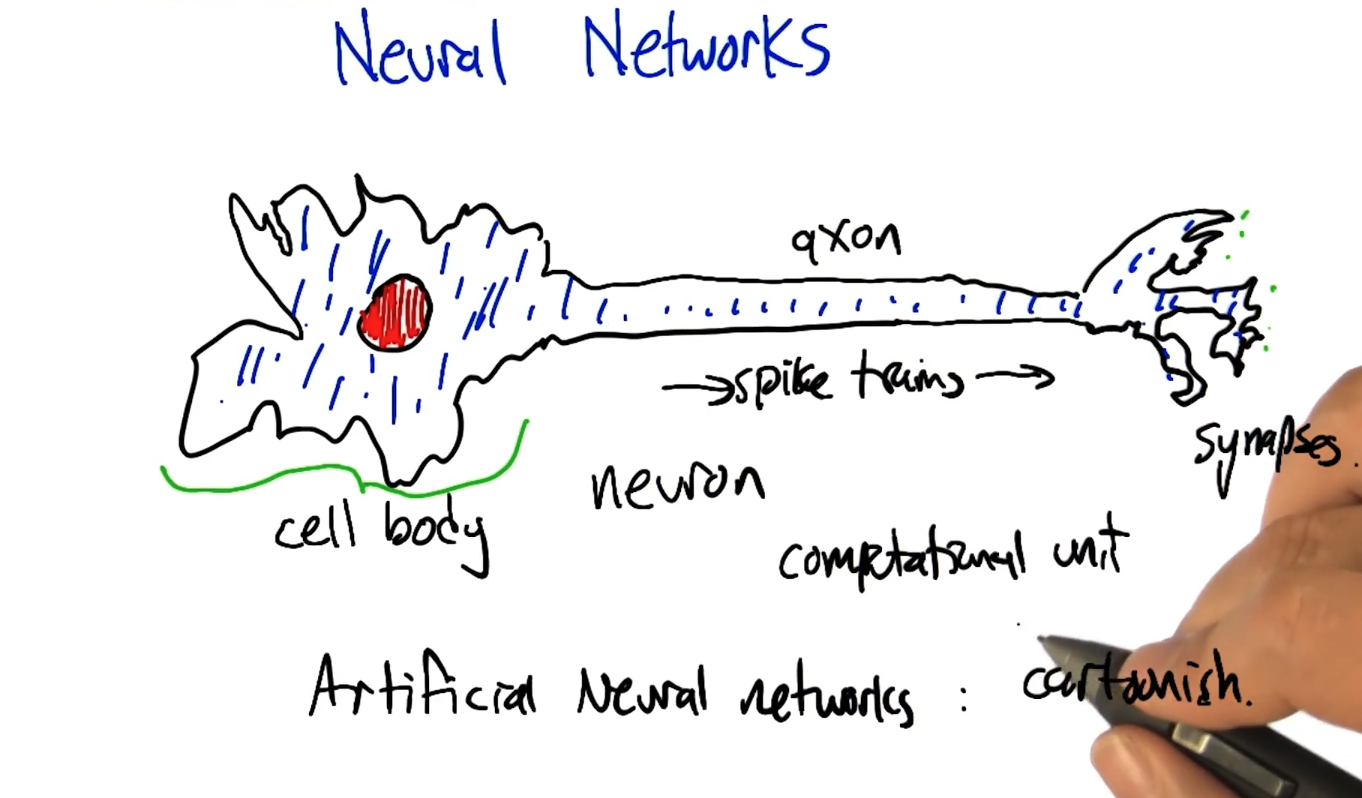
Neural Networks algorithms

Cell body -> Nevron -> Axon -> Synapses.

Perceptron

NN

Artificial Neural Networks​

NN

![ANN](../images/SL 3 - Neural Networks Artificial Neural Networks.png)

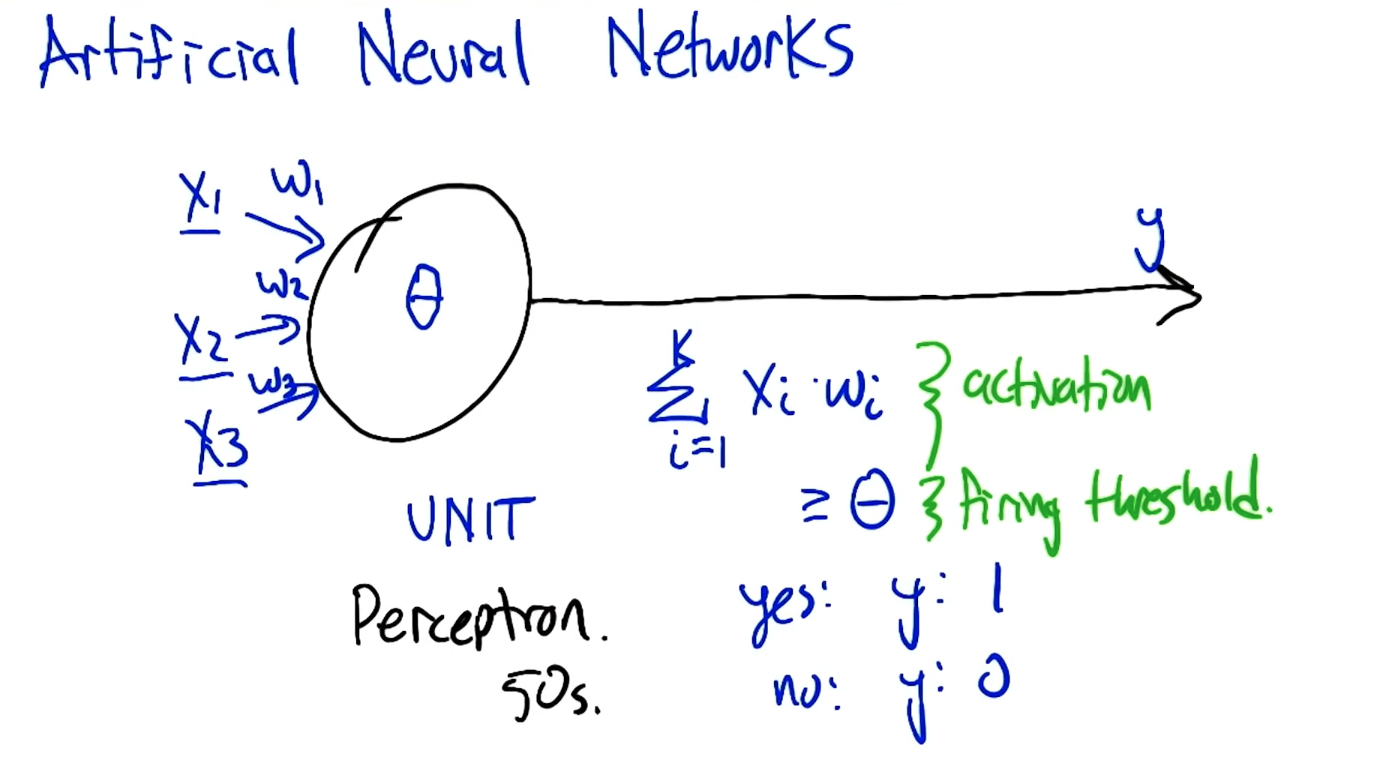
We need to pay attention to

  • Activation function
  • firing threshold

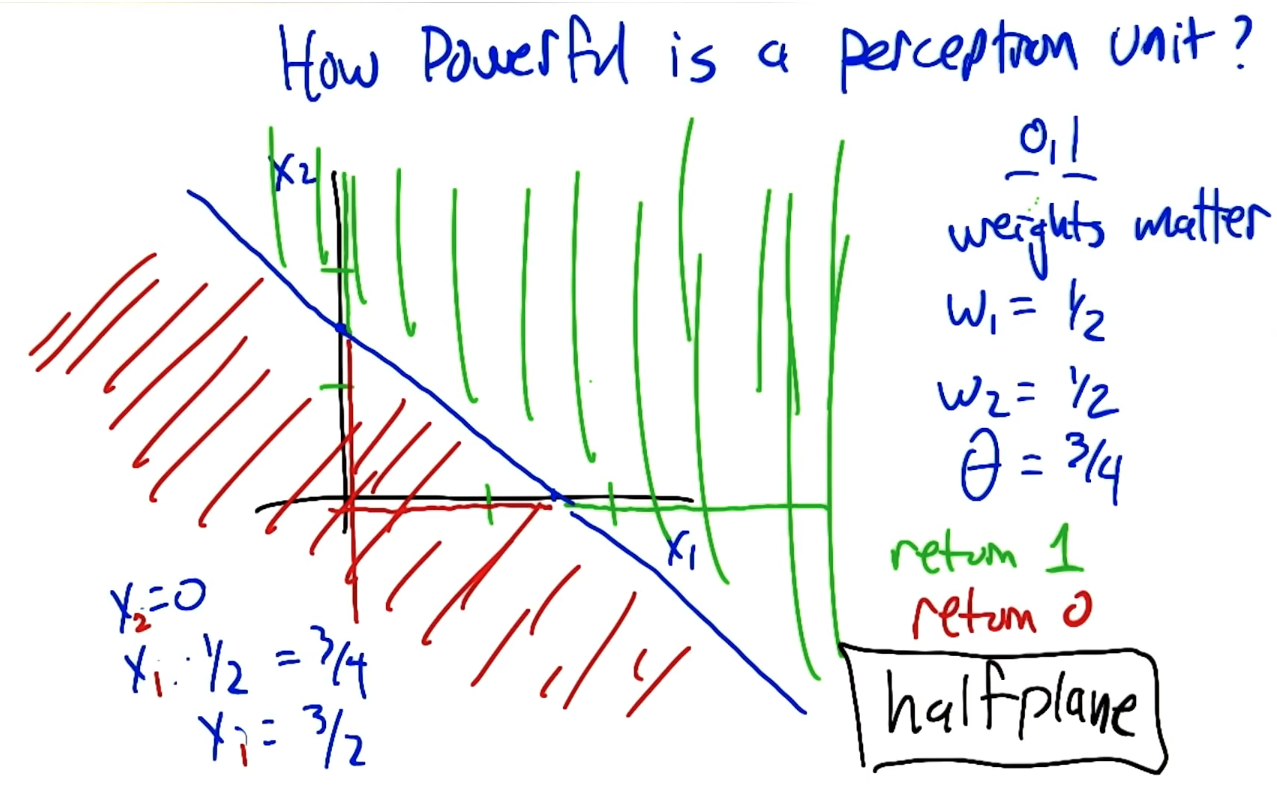
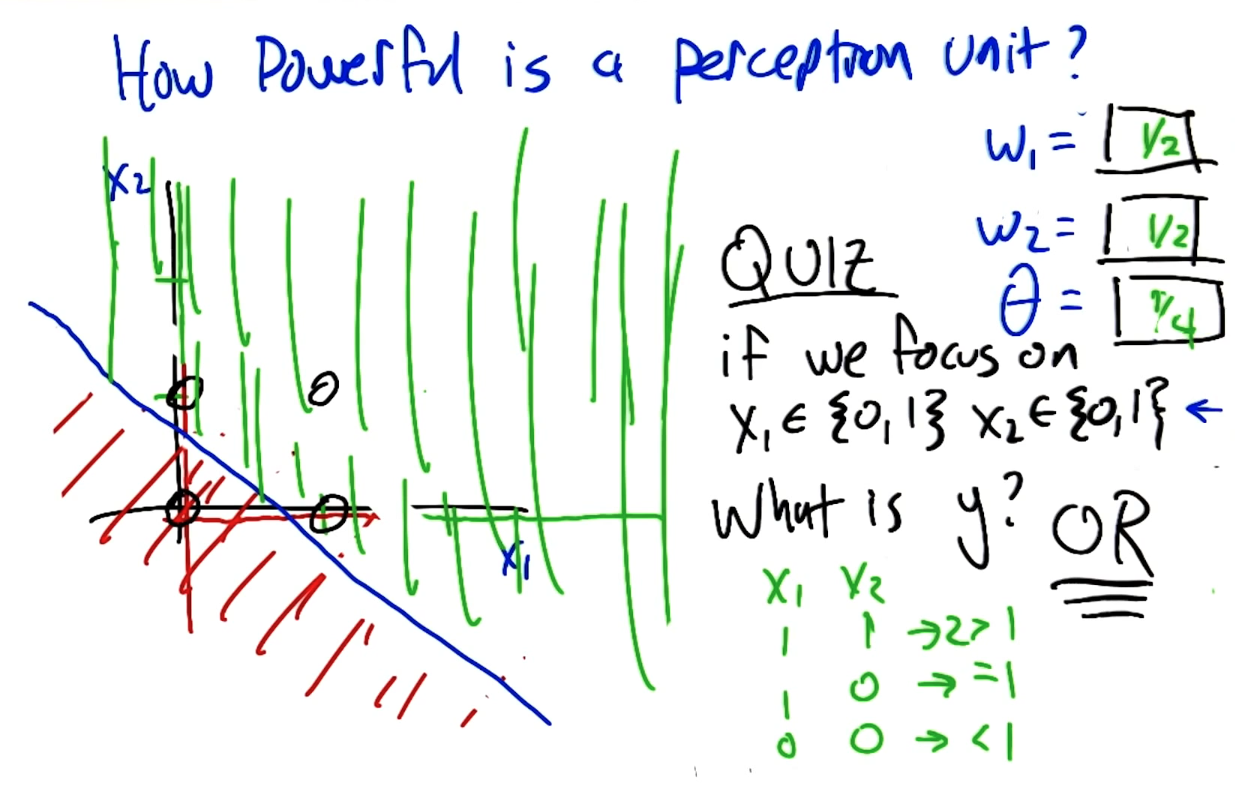
How powerful is perceptron unit?​

One activation function computes the half plane.

perceptron

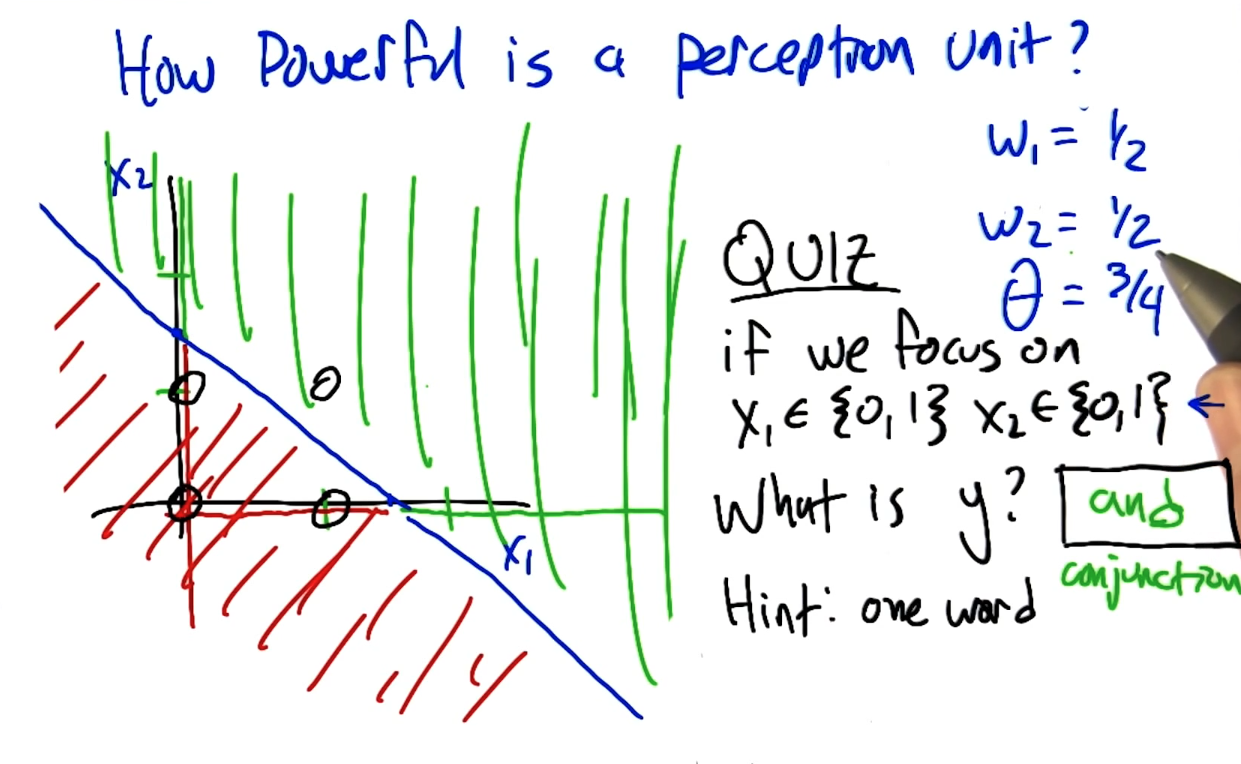
What's the nice and short computing in the following?

Boolean: AND​

perceptron_func

Boolean: OR​

OR-Func

Boolean: Not​

Unit-Not

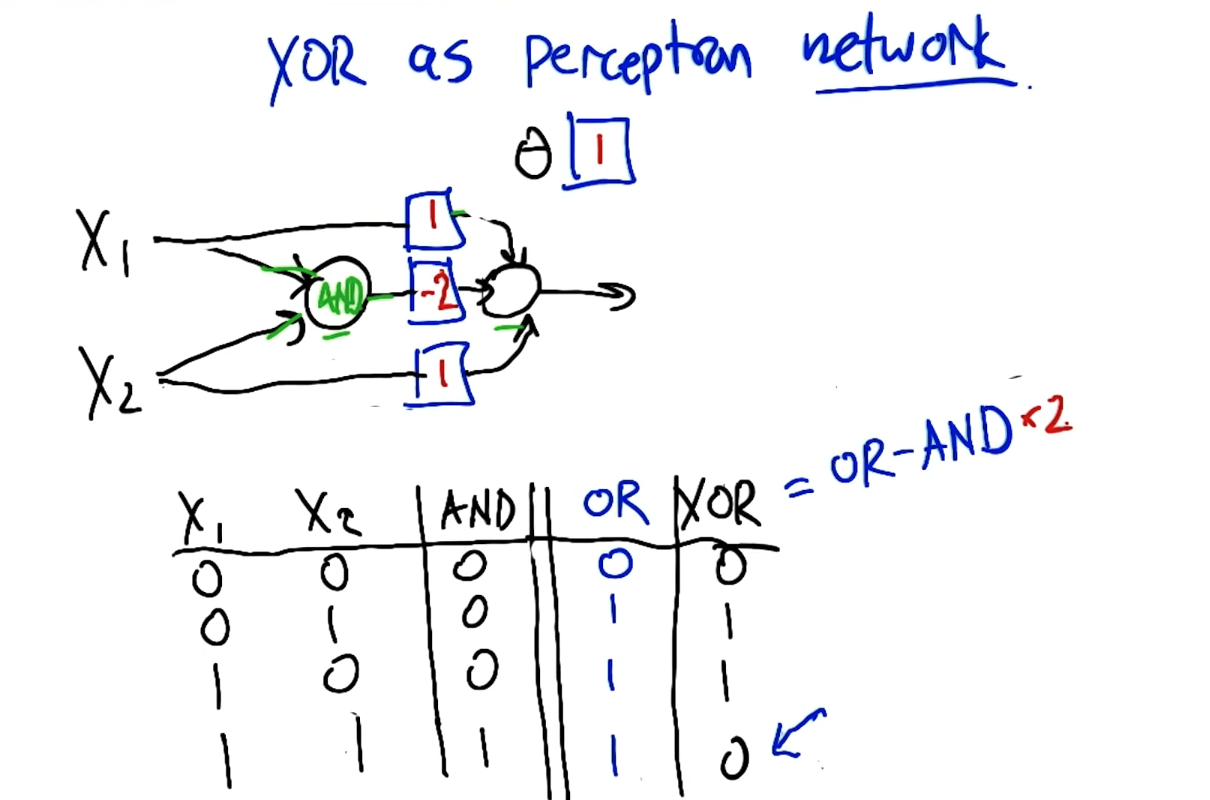
XOR as Perceptron Network​

XOR

Perceptron Training​

Given examples, find weights that map inputs to outputs.

  • Perceptron rule (threshold)
  • Gradient descent / delta rule (un-thresholded)

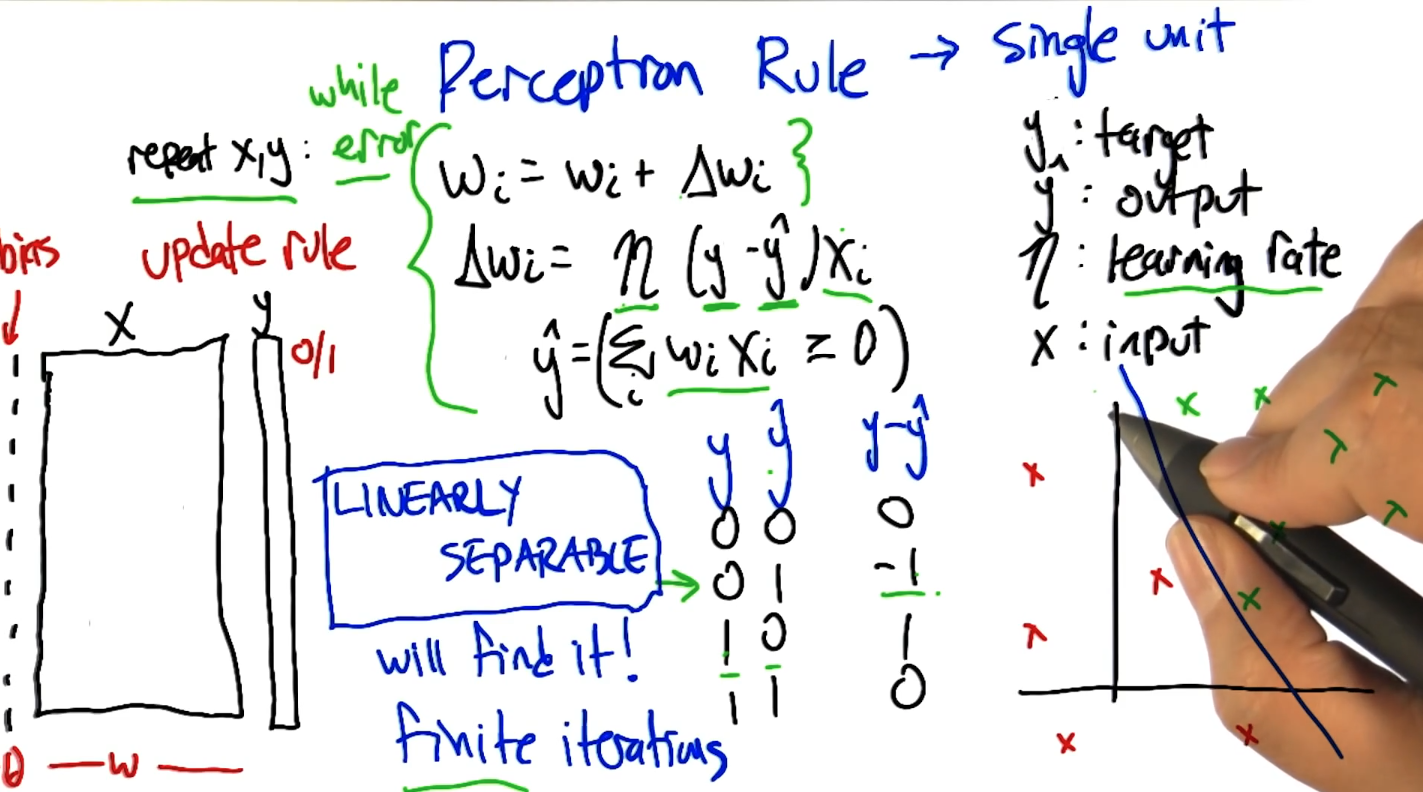
Perceptron rules​

Single Unit

The halting problem for iterations.

perceptron-training

Gradient Descent​

Avoid Non-linear separability issues.

Gradient-descent

Comparison of Learning rules​

Perceptron rule​

guarantee to finite convergence only if linear separability

ΔWi=η(y−y′)xi\Delta W_i = \eta (y - y') x_i

Eta = learning-rate

y = target

y' = output

Gradient Descent rule​

Calculus, robust, converge to local optimum

ΔWi=η(y−a)xi\Delta W_i = \eta (y - a) x_i

Comparing rules​

comparison-learning-rules

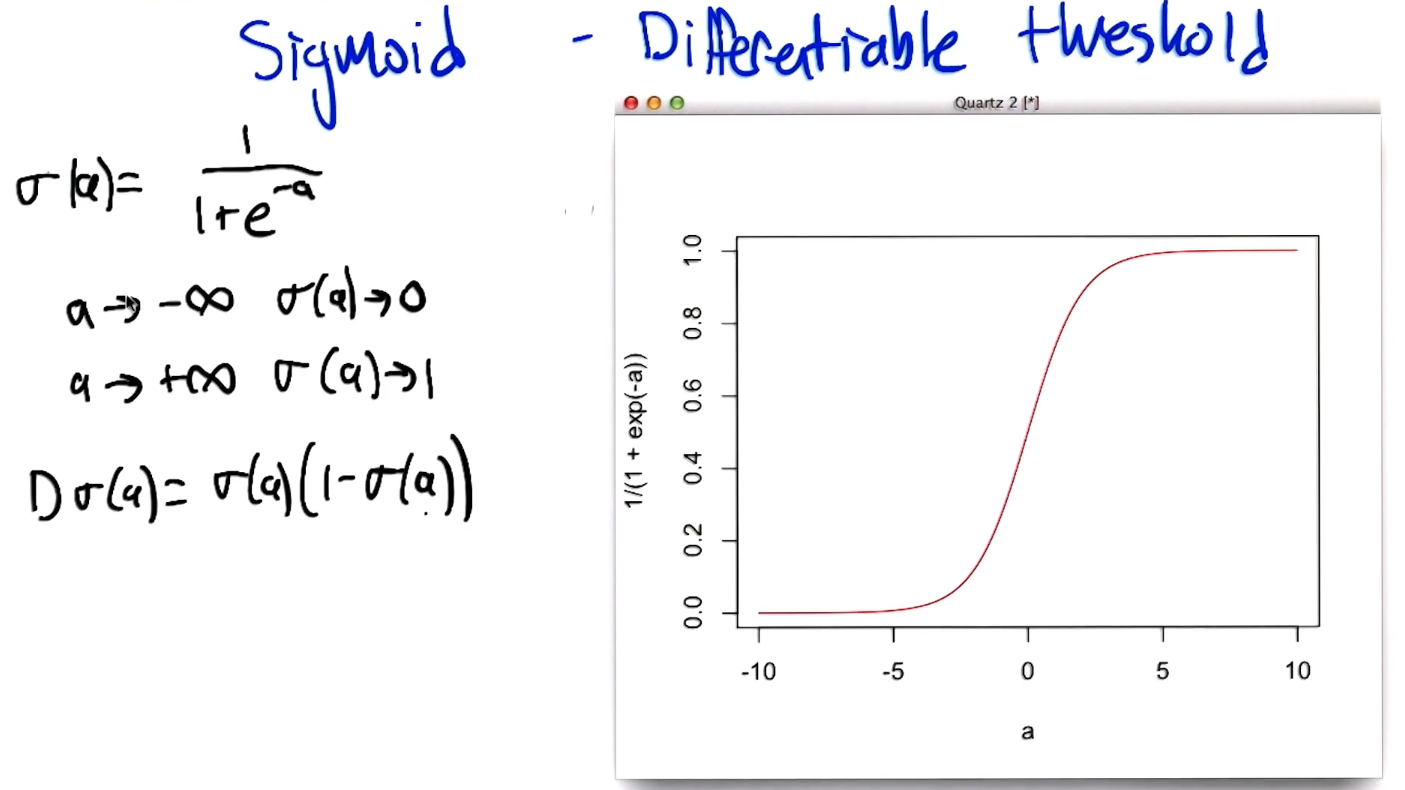
Sigmoid - differentiable threshold​

Sigmoid

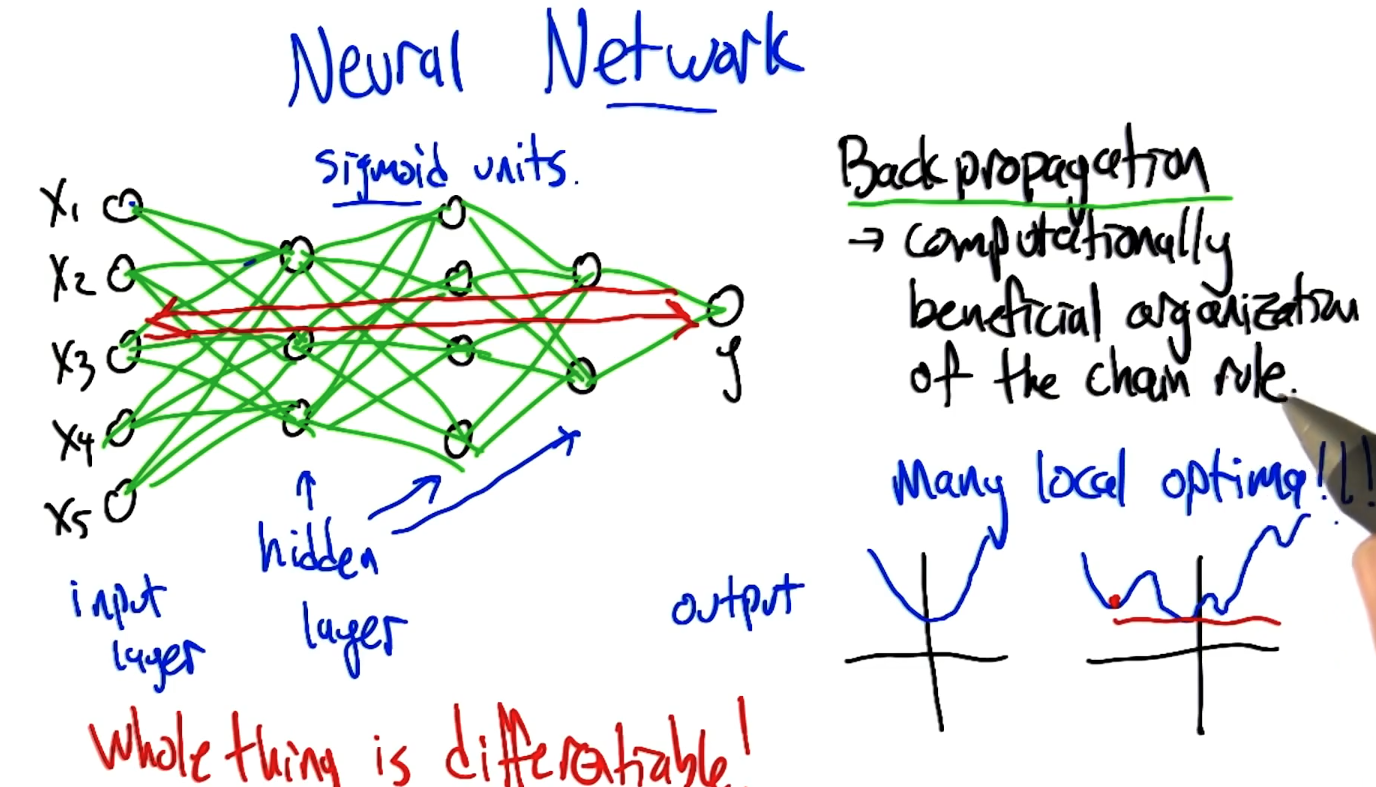
Neural Network Sketch​

Whole thing is differentiable!

Back-propagation -> computationally beneficial organization of the chain rule.

The errors flowing backwards, sometimes it's even called error back propagation.

Many local optimal!!!

SL3_Neural_network_Sketch.png

Optimizing weights​

  • Gradient descent
  • Advanced methods
    • Momentary
    • Higher order derivatives
    • Randomized optimization
    • Penalty for "complexity"

Optimization:: learning

  • More nodes
  • More layers
  • Large numbers

Restriction Bias​

SL3_Restriction_bias.png

Peference Bias​

Algorithm's selection of one representation over another.

What algorithm?

Gradient descent. We need to check initial weights. Normally, we pick up small random values. Local minimal variability

Low "complexity", simpler explanations.

Occam's razor​

Entities should not be multiplied unnecessarily.

Summary​

  • Perceptrons - threshold unit
  • Networks can produce any boolean functions.
  • Perception rule - finite time for linearly separable
  • General differentiable rule - back propagation & gradient descent
  • Preference & restriction bias of neural networks.