Skip to main content

Randomized optimization

Input space X

Objection function (fitness function) f: X->R

Goal: find

x∗fromX,f(x∗)=maxf(x)x^* from X, f(x^*) = max f(x)

Find the best.

  • Rate finding
  • Root finding
  • Neural networks x is weights minimize error.

Optimization approaches​

Generate & Tests: small input spaces, complex function

Calculus: function has derivative

Newton's method: function has derivative, iterative improve -> single optimium

what if assumption didn't hold?

Big input space, complex function, no derivative ( hard to find), possibly many local optima.

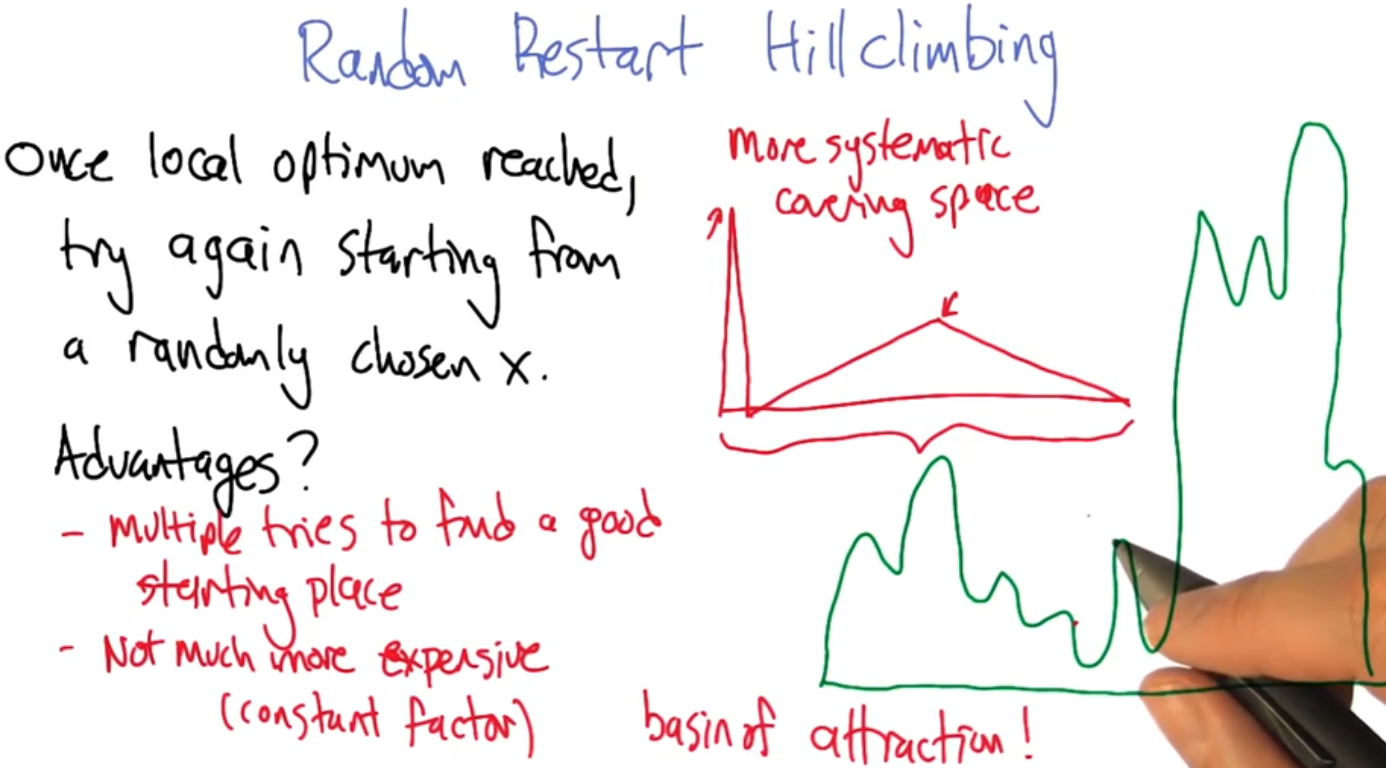
Hill climbing​

UL1_random_hill_climbing.png

Simulated Annealing​

UL1_simulated_annealing.png

Metropolis-Hastings

Genetic algorithms​

Summary​

Two problems:

  1. These algorithms didn't remember information. How to capture history?

  2. Simulated annealing uses Boltzmann distribution. How to capture probability distribution?

e.g.

  • TABU search

MIMIC​

  • Only points, no structure
  • Unclear probability distribution.

Reference: MIMIC: Finding Optima by estimating probability densities.

  • Directly model of probability distribution
  • Successfully define model.

A probability model​

MIMIC: a probability model​